こんにちは。LegalForce Researchで研究員をしている神田 (@kampersanda) です。
LegalForce Researchでは現在、高速なパターンマッチングマシン Daachorse(ダークホース)を開発・運用しています。文字列処理の基礎である複数パターン検索を提供するRust製ライブラリです。以下のレポジトリで公開されています。
本記事はDaachorseの技術仕様を解説します。具体的には、
- 複数パターン検索に関係する基礎技術(トライ木・Aho–Corasick法・ダブル配列)
- Daachorseの実装の工夫と性能
を解説します。
以下のような方を読者として想定します。
Daachorseについて
まずはじめにDaachorseの簡単な紹介をします。
Daachorseは、文字列処理の基礎である複数パターン検索を提供するRust製ライブラリです。パターンの集合とテキストを入力すると、テキストに出現するパターンを列挙することができます。その特徴としては、以下が挙げられます。
複数パターン検索には多くの応用があります。身近な例では、形態素解析器や正規表現エンジンなどです。Daachorseは非常に高速に動作するので、これらアプリケーションの高速化に寄与するでしょう。
例えば、LegalForce Researchでは高速な単語分割器 Vaporetto(ヴァポレット)を開発しており、そのコアコンポーネントとしてDaachorseを使っています。複数パターン検索は単語分割において大部分を占める処理なので、高速なVaporettoの実現には高速なDaachorseが必須です。
複数パターン検索の基礎知識
Daachorseはダブル配列を用いたAho–Corasick法の実装です。ここでは準備として、複数パターン検索、トライ木、Aho–Corasick法、ダブル配列を解説します。
複数パターン検索
複数パターン検索とは、入力として文字列パターン集合とテキストが与えられると、テキストに含まれるパターンとその位置のペアをすべて報告する問題です。
例えば、4つのパターン 世界,世界の,全世界,国民 を用いてテキスト 全世界の国民が を検索すると、下線で示された4つの出現が報告されます。

本記事では、例の 全世界,世界,世界の のように出現位置のオーバラップを許す問題を取り扱います。応用によっては、オーバラップを許さない問題設定もバリエーションとして考えられますが、本記事では取り扱いません。しかし、Daachorseではそのような検索も提供しています。興味のある方はDaachorseのREADMEをご参照ください。
トライ木
複数パターン検索を解くアルゴリズムとしてトライ木を使った方法があります。次に紹介するAho–Corasick法の基礎となるアルゴリズムです。
トライ木はパターンの集合を保存するデータ構造で、パターンの接頭辞を併合して構築されるオートマトンの一種です。下図に例を示します。

トライ木は枝に文字を付随し、文字を使って状態を遷移します。トライ木の状態はいずれかのパターンの接頭辞に対応し、根からその状態までの経路上の文字を連結することで接頭辞は復元されます。例えば、状態 2 は 世界 を表し、状態 0 → 1 → 2 の経路上の文字を連結することで 世界 は復元できます。
パターンに対応する状態を出力状態と呼び、灰色で描画しています。例えば、状態 2 は出力状態なので、世界 がパターンとして登録されていることがわかります。
トライ木による共通接頭辞検索
あるパターンがトライ木に登録されているかどうかは、その文字を使って根から状態を遷移し、最終的に訪れた状態が出力状態かどうかを調べることで確認できます。その状態が出力状態でなかったり、途中で遷移に失敗した場合は、そのパターンはトライ木に登録されていません。
例えば、パターン 世界の が登録されているかどうかは、下図のように状態 0 から 3 まで遷移し、状態 3 が出力状態であるかことから確認できます。

ここでのトライ木の特徴は、検索パターンの接頭辞も同時に、パターンとして登録されているかを知ることができることです。これは、遷移中に訪れた状態が出力状態かを調べることで実現されます。例えば、 世界の の検索中に状態 2 を訪れますが、状態 2 が出力状態であることから接頭辞の 世界 もパターンとして登録されていることがわかります。
このように検索パターンのすべての接頭辞について、トライ木に登録されているかを調べる検索を共通接頭辞検索と言います。
トライ木による複数パターン検索
トライ木を用いた複数パターン検索は、テキストの各位置を起点とした文字列について、共通接頭辞検索をすることで実現されます。例えば下の図は、テキストの位置 2 から開始する文字列について共通接頭辞検索をしたときの例です。テキストの位置 2 からは、 世界 と 世界の がパターンとして出現することがわかります。

このように、テキストのすべての位置を起点として共通接頭辞検索を実行することで、テキストに出現するパターンを漏れなく検索することができます。パターンの最大長を m とすると、共通接頭辞検索は O(m) 個の状態を遷移します。そのため、テキスト長を n とすると、トライ木を用いた複数パターン検索は O(nm) 時間で動作します。
Aho–Corasick法
トライ木による複数パターン検索の欠点は、一つ前の共通接頭辞検索で読み込んだテキストの内容を捨ててしまう点です。例えば以下のように、テキストの先頭位置からの共通接頭辞検索で 全世界の までを読み込んだのに、次の検索ではその読み込み位置を巻き戻して 世界の... から改めて検索し直します。

しかし 全世界 を読み込んで状態 6 まで遷移できた時点で、次の検索で 世界 という文字列を使って状態 2 まで遷移することは、登録されているパターン集合から明らかです。状態 6 から状態 2 までにポインタを渡せば、 世界 というテキストの再読み込みを回避できそうです。
Aho–Corasick法はこのようなアイデアに基づき、トライ木に追加の情報を持たせることでテキストの再読み込みを回避するアルゴリズムです。下図のようなトライ木を拡張したオートマトン(ACマシン)を使って検索を実現します。
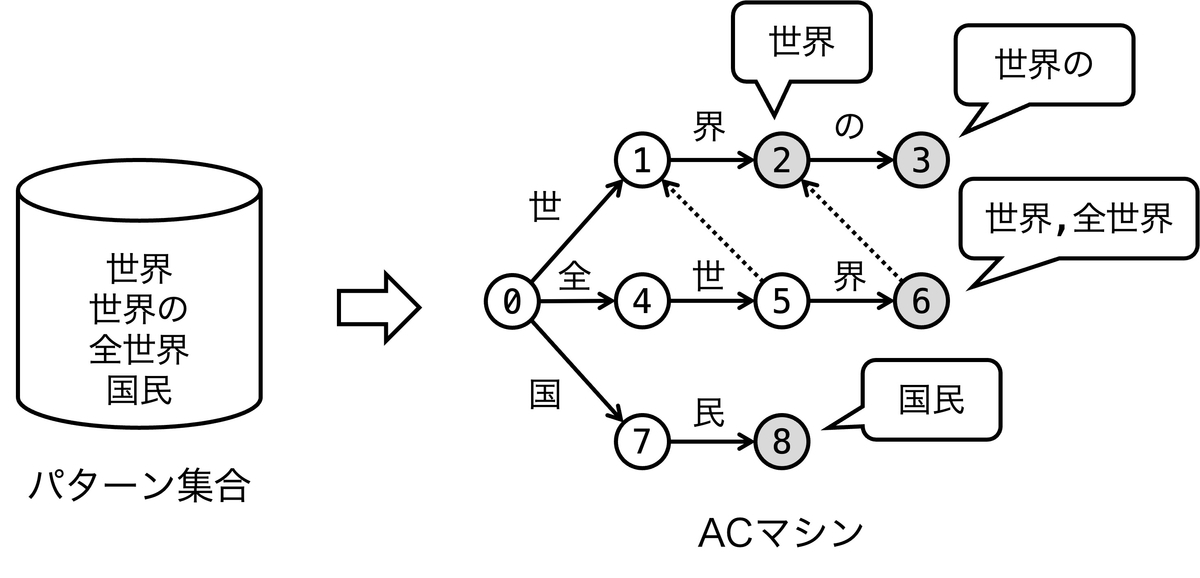
トライ木の例と比べて、破線の矢印が追加で描画されています。これを接尾辞リンクと呼びます。
接尾辞リンクを簡単に説明します。ある状態の接尾辞リンクは、その状態が表す文字列の接尾辞のうち、最長の接尾辞を表す別の状態を指すように定義されます。例えば、状態 6 が表す 全世界 の接尾辞 世界,界 のうち、最長の 世界 を表す状態 2 への接尾辞リンクが定義されます。接尾辞には空文字列も含まれるので、いずれの状態にも空文字列を表す根への接尾辞リンクが少なくとも定義されます。ただし、上図では根への接尾辞リンクの描画は省略しています。
加えて、ACマシンでは各状態が出力するパターンの集合を保持します。これを出力集合と呼びます。ある状態の出力集合は、その状態から接尾辞リンクを使って辿ることのできる出力状態が表すパターンの集合です。例えば、状態 6 は 世界 を出力に持つ状態 2 を辿れるので、 世界,全世界 を出力集合として持ちます。
ACマシンによる複数パターン検索
ACマシンによる複数パターン検索は、トライ木のアルゴリズムと同じようにテキストを一文字ずつ読み込みながら状態を遷移します。違う点は遷移に失敗したときの処理です。トライ木では根まで巻き戻って検索を再開していたのに対して、ACマシンでは接尾辞リンクを辿って遷移を継続します。
以下の検索例を見てみましょう。 全世界 で検索し状態 6 まで遷移する様子はトライ木の例と同じです。状態 6 を訪れたところで、この状態は出力集合を持つのでパターン 世界,全世界 を出現として報告します。次に、文字 の で遷移を試みますが、遷移先状態が無いので検索は失敗します。ここで、ACマシンは接尾辞リンクを辿って状態 2 に移動し、再び の で遷移を試みます。今度は遷移先として状態 3 が見つかるので、検索を続行します。

このように、ACマシンは接尾辞リンクと出力集合を利用することで、テキストの読み込み位置を巻き戻すことなく複数パターン検索を実現します。テキスト長を n と解の個数を occ としたとき、検索は O(n+occ) 時間で動作します。
Aho–Corasick法は線形時間という優れた理論保証を持つ一方で、実際の検索速度はACマシンを表現するデータ構造に大きく影響します。これから説明するダブル配列は実用に優れたデータ構造であり、高速なACマシンの実装を可能にします。
ダブル配列
ダブル配列はトライ木を表現するための高速なデータ構造です。BASEとCHECKの2つの配列により状態を表現します。BASE・CHECK配列の各要素が状態に対応し、そのオフセット値が状態のIDになります。つまり状態 s には BASE[s], CHECK[s] が対応します。
状態 s から状態 t への文字 c による遷移について、以下の2式(遷移式)を満たすようにBASE・CHECK値は決定されます。
- BASE[s] + Code(c) = t
- CHECK[t] = s
ここで、Code(c) は文字 c に割り当てられた整数のコード値です。
この遷移式を図で表すと以下のようになります。状態 s から文字 c で遷移した先の状態のID t は、そのBASE値とコード値の足し算によって算出できます。そして、その遷移先状態 t のCHECK値が遷移元状態 s を指すとき、遷移が正しく定義されていることが確認できます。

「トライ木」節で例示したトライ木を、ダブル配列により表現した例を以下に示します。ただし出力として、パターン文字列の代わりに、そのIDを格納しています。
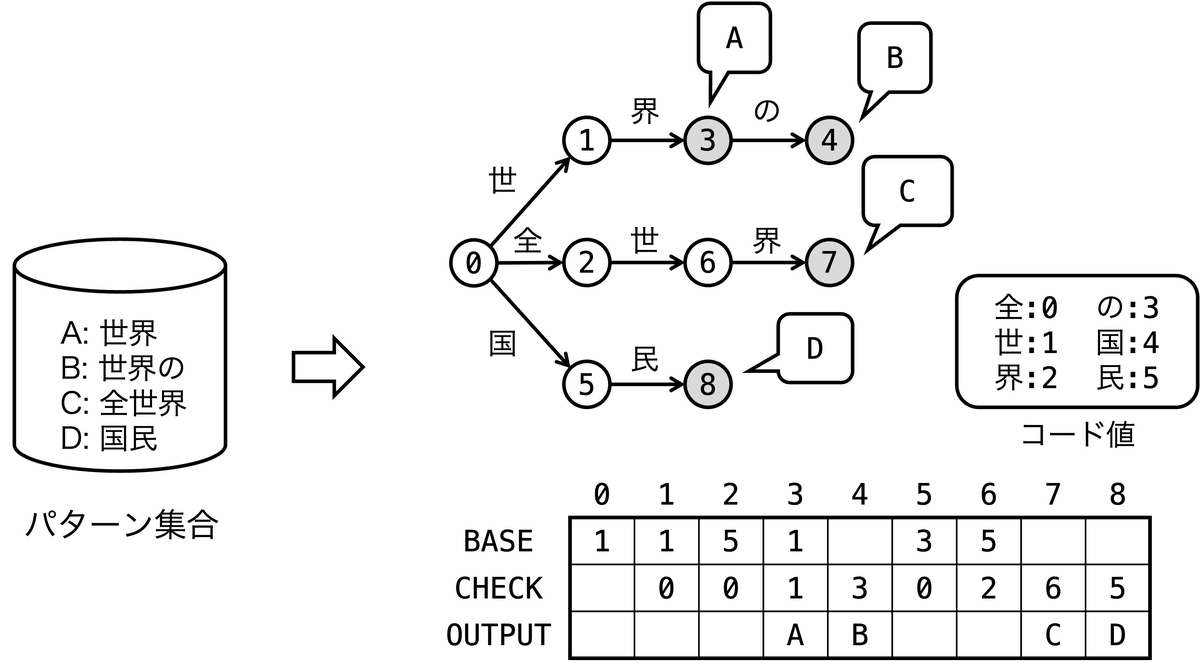
ダブル配列の遷移式を満たすように状態にIDが割り当てられ、BASE・CHECK値が決定されています。OUTPUT[s]は状態 s の出力を保存するための配列です。
例えば、状態 6 から文字 界 による遷移先は
- BASE[6] + Code(
界) = 5 + 2 = 7 - CHECK[7] = 6
なので状態 7 であることがわかります。
一方、状態 6 から文字 全 による遷移は
- BASE[6] + Code(
全) = 5 + 0 = 5 - CHECK[5] ≠ 6
なので定義されていないことがわかります。
ダブル配列の利点は、例からも分かるように単純な足し算と条件分岐だけで状態の遷移が実現できることです。実用において非常に高速なトライ木の遷移を実現します。
ACマシンの表現
ACマシンはトライ木のシンプルな拡張なので、ダブル配列でも表現することができます。トライ木との違いは、各状態が接尾辞リンクと出力集合を保持する点です。
上図のACマシンをダブル配列で表現した例を下図に示します。
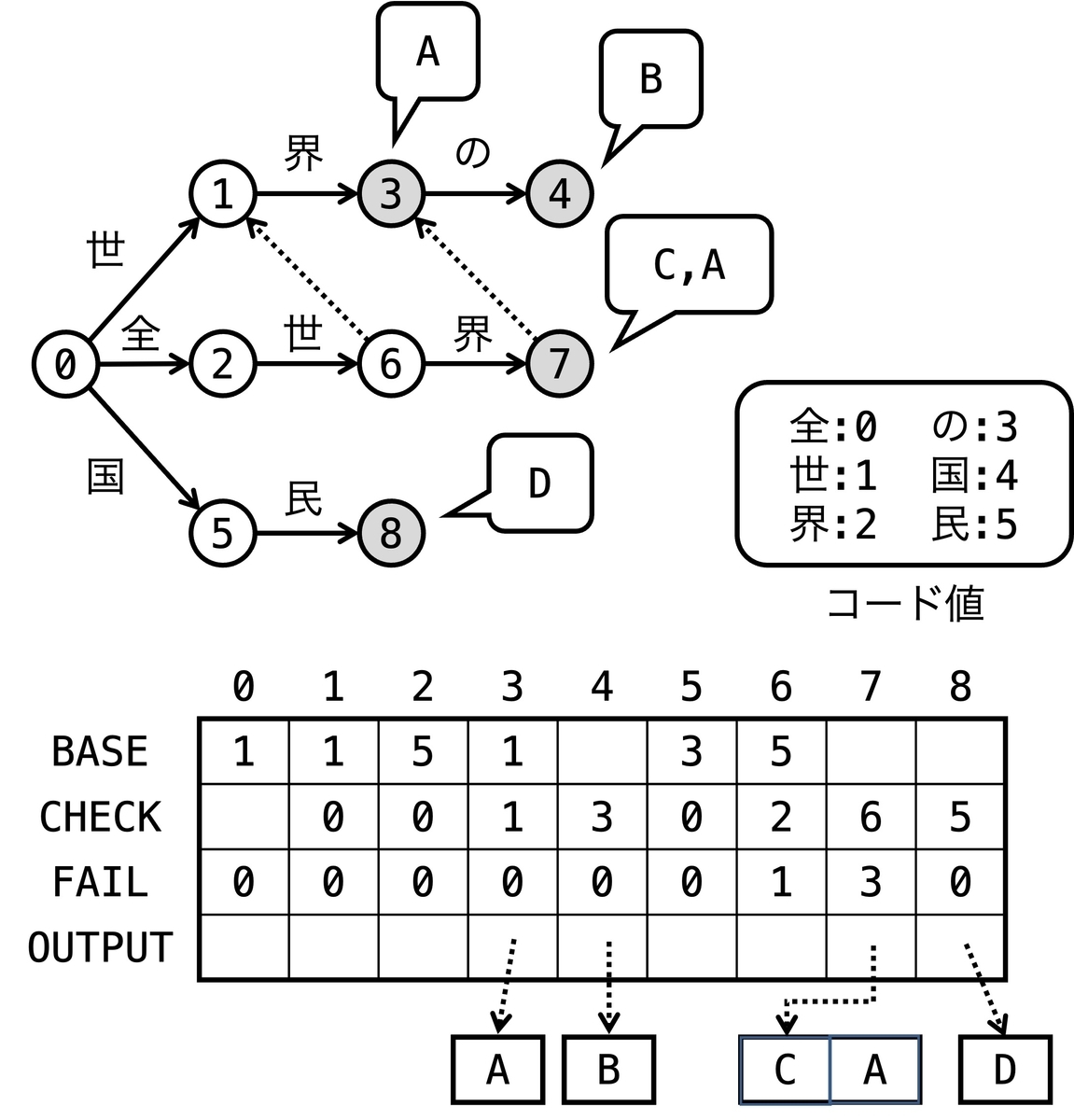
FAILは接尾辞リンクを格納した配列です。OUTPUTは状態に対応する出力集合へのポインタを保持した配列です。出力集合は配列として保存されています。
Daachorse 効率化の工夫
Daachorseは、上記したようなダブル配列を用いたACマシンの実装です。そして、その性能を最大限に引き出すために入念に実装されています。ここでは、その工夫した点について解説します。
メモリ効率の良い出力集合の保存
ここでは、効率的な出力集合の保存方法を考えます。最もシンプルな方法は、下図のように出力集合を配列として保存し、出力状態に配列へのポインタを格納する方法でしょう。

例えば、状態 7 の出力集合 {C,A} は OUTPUT[7] が指す配列を参照することで得られます。この方法は、配列をスキャンするだけで出力集合が復元できるので参照の局所性が良いです。しかし、 A のような重複する出力値を保存する必要がありメモリ効率が悪いです。
Daachorseの設計
Daachorseでは、そのような重複する出力値を併合して保持することで、上記の方法のメモリ効率を改善します。具体的には、以下のような事実に基づいて出力集合を併合します。
| 事実 |
|---|
| 状態 s から接尾辞リンクを通して状態 t に到達できるとき、状態 t の出力集合は状態 s の出力集合の部分集合である。 |
例えば、状態 7 から接尾辞リンクを通して状態 3 に到達できるので、状態 3 の出力集合 {A} は状態 7 の出力集合 {C,A} の部分集合です。
この事実に基づけば、状態 t の配列は状態 s の配列の部分配列として表現できます。例えば下図のように、状態 3 の配列は、状態 7 の配列の後方部分で表現できます。つまり、OUTPUT[3] には状態 7 の配列の途中を指すポインタを格納すればよいです。

この方法により、保存する出力値の数を減らしてメモリを節約することができます。例えば本記事の実験で使用したデータセットでは、保存する出力値の数が20—40%少なくて済みます。
追記:v0.4.2で森構造を使った別の表現に置き換わりました。詳しくは論文の節3.1をご参照ください。
Bytewise & Charwise Daachorse
Daachorseでは、文字列をバイト列として扱うBytewise Daachorseと、ユニコード列として扱うCharwise Daachorseの2種類の実装を提供しています。Bytewise Daachorseは文字列のエンコードに依らず適用できる汎用的な実装で、Charwise Daachorseは日本語などのマルチバイト文字列に特化した実装です。
例えば 世界 というマルチバイト文字列は、それぞれの実装で以下のように処理されます。Bytewise Daachorseでは、UTF-8で 0xE4,0xB8,0x96,0xE7,0x95,0x8C の6バイトで表現し、6個の遷移を定義します。Charwise Daachorseでは、ユニコードで U+4E16,U+754C の2つのコードポイント値として表現し、2個の遷移を定義します。

例からも分かるように、マルチバイト文字列についてはCharwise Daachorseの方が少ない状態数でACマシンを構築でき、少ない遷移回数で検索できます。コード値が取りうる範囲は大きくなりますが、ダブル配列の遷移は定数時間なので影響ありません。そのため、日本語などのマルチバイト文字列からACマシンを構築する場合、Charwise Daachorseを使った方が高速な検索が期待できます。
ただし注意点として、状態から出る遷移数が多くなると、ダブル配列の構築が低速化しやすくなるという問題があります。ダブル配列の構築では、遷移式を満たすように配列の空要素を探索して状態を配置します。このとき、状態から出る遷移数が多いと空要素を見つけるのが難しくなり、結果として構築が低速化します。また、データセットによっては空要素が多くなりメモリ効率が悪くなります。
バイト列では状態から出る遷移数が256個で抑えられます。そのため、バイト列から構築することで、空要素がほとんど無いダブル配列を高速に構築できることが経験的にわかっています。文字列のエンコードに関わらず適用できるなどの利点もあるため、Dartsを始めとする多くのライブラリがBytewiseを採用しています。
使い分け基準
まとめると、Bytewise/Charwise Daachorseは以下の特徴に注意して使い分けることをオススメします。
- Bytewise Daachorseはどんな文字列についても安定した性能を提供する
- Charwise Daachorseはマルチバイト文字列について高速な検索を提供するが、構築が低速なことに注意
Bytewise Daachorseの要素圧縮
BASE・CHECKは配列のオフセット値を格納するので、一般的に要素当たり4バイトを割り当てて実装します。しかし文献 3 の圧縮法を適用することで、オフセットの代わりにコード値をCHECK配列に格納することができます。
すなわち下図のように、遷移先 t のCHECK値に遷移元 s を格納する代わりに、遷移に使ったコード値 Code(c) を格納します。

ただし不正な遷移を回避するために、任意の状態ペア (s,s’) について BASE[s] ≠ BASE[s’] を満たす必要があります。
バイト列から構築するとき、コード値は 1 バイトで表現できます。Bytewise Daachorseはこの圧縮法を採用し、CHECK配列の要素当たりのサイズを 4 バイトから 1 バイトに圧縮しています。
参照の局所性を考慮した配列構造
ダブル配列の説明では、便宜上「BASEとCHECKの2つの配列」という表現を使っていますが、実際には「BASE値とCHECK値をメンバに持つ構造体の配列」として実装するのが効率的です。ダブル配列の遷移では、BASE[s]とCHECK[s]は連続して参照されるので、参照の局所性を考慮しての実装になります。

Daachorseでも同じように「BASE値・CHECK値・FAIL値・OUTPUT値をメンバに持つ構造体の配列」として実装しています。このとき、データ構造アライメントを考慮して、各値の表現に何バイトを割り当てるのかを考える必要があります。
Charwise Daachorseでは各値がオフセット値なので、その表現に4バイトを割り当てます。つまり、配列の要素は16バイトで表現されます。これは、4バイトアライメントでメモリをパディングすること無くシンプルに実装することができます。
一方でBytewise Daachorseでは、CHECK値を1バイトに圧縮しているので、同じようにオフセット値に4バイトを割り当てると、配列の要素は13バイトで表現されることになります。この要素を4バイトアライメントでパディング無く実装するために、Bytewise DaachorseではFAIL値を3バイトに削減し、要素を12バイトで表現しています。
この修正により、Bytewise DaachorseはFAIL値を3バイトで表現できないような大きいACマシンを表現できなくなります。しかしAho–Corasick法の応用を考えたときに、それほど大きなACマシンを表現する需要はあまりないと判断して、このような実装を採用しています。
FAIL・OUTPUTの埋め込み検討
上の例で示したダブル配列では、BASE・CHECK・FAIL・OUTPUTの4個の配列によりACマシンを表現しています。しかしデータセットによっては、FAILの多くの値が初期状態を指し、OUTPUTの多くの要素がポインタを持ちません。これらのメモリを節約するために、既存のダブル配列の実装では、特殊文字によって遷移される状態を定義し、FAIL配列やOUTPUT配列を削除することを検討しています(例えば、文献 4)。
具体的には、初期状態以外の接尾辞リンクを持つ状態からは特殊文字 $ により遷移する状態を、出力状態からは特殊文字 # により遷移する状態を定義します(下図)。

特殊文字により新たに定義された状態は遷移先を持たず、それらのBASE値は必ず未使用になります。そのため、ポインタをBASE値に埋め込むことができ、FAIL・OUTPUT配列を削除することができます。一方で、状態数が増えることとポインタの取得に遷移を要することが欠点となります。
Daachorseの設計
Daachorseを設計するに当たって、日本語テキスト解析用辞書UniDicに含まれる重複を除く68万単語からCharwiseにACマシンを構築した場合の統計値を調べました。その結果、99%程度の状態が初期状態以外を指す接尾辞リンクを保持し、99%程度の状態が出力集合へのポインタを保持していました。つまりUniDicの場合、FAIL・OUTPUT配列を削除する利点はありません。
もちろん、この結果はデータセットに依存するものです。しかし、Daachorseは第一にVaporettoの高速化を目的としたライブラリなので、自然言語辞書による結果を優先し、BASE・CHECK・FAIL・OUTPUTの4個の配列を用いた実装にしています。
Daachorseのベンチマーク
Daachorse v0.4.0と他のRust製パターンマッチングライブラリとの比較結果を示します。比較するライブラリは以下の3つです。
- aho-corasick (v0.7.18): Rustで最も有名なAC法の実装
- fst (v0.4.7): 有限状態トランスデューサを用いた辞書の実装
- yada (v0.5.0): ダブル配列を用いたトライ木の実装
aho-corasickライブラリはNFA型とDFA型の2種類の実装を提供しています。NFA型は通常のACマシンの実装です。DFA型は、ACマシンのすべての状態と文字の組み合わせについて、遷移を展開し陽に保存した実装です。DFA型はNFA型より少ない状態遷移で検索できるので高速ですが、膨大なメモリを使用します。
データセットとしては、以下の2通りを使用しました。
- Word100K
- パターン集合: 英単語10万件 from fstライブラリ
- 検索テキスト: The Adventures of Sherlock Holmes from Project Gutenberg
- UniDic
より詳細な実験設定や他の検索オプションでの結果については、レポジトリのWikiをご参照ください。
結果
検索時間
テキストに出現するパターンをすべて列挙するのに所要した時間を以下に示します。

両データセットにおいて、daachorseが高速なことがわかります。Word100Kではaho-corasick (DFA)が最速で、次点でdaachorseが高速でした。DFA型はリッチにメモリを確保しているので高速ですが、daachorseもそれに接近しています。yadaも非常に高速であり、ダブル配列の時間効率の良さが伺えます。UniDicではdaachorse (charwise)が突出して高速であり、CharwiseにACマシンを構築することの重要性が伺えます。
メモリ使用量
オートマトンのメモリ使用量を以下に示します。
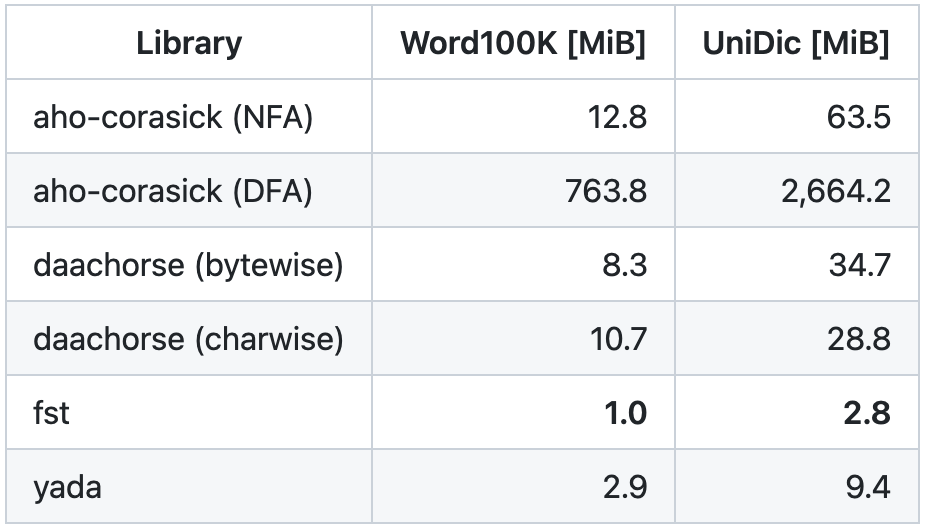
ACマシンは有限状態トランスデューサやトライ木と比べて多くのデータを持つので、メモリ使用量は大きくなります。しかし、同じAho–Corasick法の実装であるaho-corasickと比べると、daachorseは少ないメモリ使用量なのがわかります。
まとめ
本記事では、ダブル配列を用いたAho–Corasick法の実装であるDaachorseを紹介しました。DaachorseはAPIもシンプルなので、お手元のRustコードに簡単に組み込んで使って頂けます。複数パターン検索は非常に基本的な問題の一つなので、高速な文字列処理が必要な多くの場面で活躍するはずです。
Daachorseはオープンソースソフトウェアなので、自由な利用はもちろん、改善の依頼やコードの提供も受け付けております。
また LegalForce Research では、コーディングが好きなソフトウェアエンジニアや研究が好きなリサーチエンジニア、チームのマネジメントをするエンジニアリングマネージャを募集しています。主に自然言語処理の分野でソフトウェアを開発したい方や、大量の文書を利用した研究をしたい方の応募をお待ちしております。
参考文献
-
Aho and Corasick. Efficient string matching: an aid to bibliographic search. Communications of the ACM, 1975.↩
-
Aoe. An efficient digital search algorithm by using a double-array structure. IEEE Transactions on Software Engineering, 1989.↩
-
Yata, Oono, Morita, Fuketa, Sumitomo, and Aoe. A compact static double-array keeping character codes, Information Processing & Management, 2007.↩
-
信種, 森田, 泓田, and 青江. ダブル配列を用いたマシンACの効率的格納手法. 言語処理学会第13回年次大会, 2007年.↩